动态规划

简介

Dynamic programming，简称DP。通过把原问题分解为相对简单得子问题得方式求解复杂问题的方法。动态规划常常适用于有重叠子问题喝最优子结构性质的问题。一般这些子问题很相似，可以通过函数关系递推出来，然后动态规划致力于解决每一个子问题一次。减少重复计算，如斐波那契数列可以看做入门级的经典动态规划。主要大的基本思想就是一个记住过去，来就现在求值。

动态规划的青蛙跳阶问题。

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法。

具体思路就是，在跳上n格的时候，你必须柯一是跳上n-1格子的次数，然后再跳上n格。
所以说需要的是记住之前的所有值来计算最新的值。从而达到在计算第n个格时候，能够以较快的速度知道。跳到n个的次数。

那么就有了斐波那契数列的应用

f(10) = f(9) + f(8)
f(9) = f(8) + f(7)
f(8) = f(7) + f(6)
f(7) = f(6) + f(5)
f(6) = f(5) + f(4)
···
f(3) = f(2) + f(1)

通用的公式为f(n) = f(n-1) + f(n-2)

然后就可以用递归来解决这个问题。

Class Solution{
public int numWays(int n){
if(n<=1){
return 1;
}
if(n==2){
return 2;
}
return numWays(n-1) + numWays(n-2);
}
}

但是用递归的方法，耗时就很大，但计算f(10)的时候，就需要先计算出子问题f(9)和f(8)然后计算f(9),又要先算出子问题f(8) 和 f(7),以此类推。一直到f(2)和f(1),递归树才结束。所以就有有了：

  • 递归复杂度 = 解决一个子问题时间* 子问题个数
  • 一个人子问题时间 = f（n-1）+f（n-2），所以复杂度是O（1）；
  • 问题个数 = 递归树节点的总数，递归树的总节点 = 2^n-1，所以复杂度是O（2 ^ n）

因此青蛙跳阶的递归解法的时间复杂度 = O(1)*O(2 ^ n) = O(2 ^ n) ,然后你会发现回过头来，有大量的重复计算，比如f(8) 被计算了两次，f（7）被重复计算了3次…..所以这个递归算法低效就是这样的原因。

带备忘录的递归解法

既然发现了存在大量的重复计算，那么就有了一个思想，我们能把重复计算的值给记录下来，当到了可以使用的时候就可以把它重新取出来使用，这样就不用有重复的计算了。所以这里又引出了一个新的问题，用什么的数据类型或者数据结构去记录这个重复的值。

  • 一般都会想到使用一个数组或者一个哈希Map充当这个备忘录。

子问题个数 = 树节点数=n，解决一个子问题还是O（1）,所以带备忘录的递归算法的时间复杂度是O（n）。接下来呢，就用备忘录的递归算法去些代码。来解决青蛙的超时问题。

public class Solution{
//使用哈希map，充当备忘录的作用
Map<Integer,Integer> tempMap = new HashMap();
public int numways(int n){
// n = 0 也算一种
if(n==0){
return 1;
}
if(n<=2){
return n;
}
//先判断有没有计算过，即看看备忘录有没有
if(tempMap.containsKey(n)){
//备忘录有，计算过，直接返回
return tempMap.get(n);
}else{
//备忘录没有，即没有计算过，执行递归计算，并且把结果保存到备忘录map中，对100000007取余
tempMap.put(n,(numWays(n-1)+numWays(n-2)) % 1000000007);
return tempMap.get(n);
}
}
}

动态规划

思路上基本和带着备忘录的递归解法是一致的，都是减少重复计算，时间复杂度也都是差不多，但是：

  • 备忘录的递归，是从f(10)往f(1)方向延伸求解的，所以称为自顶向下的解法。
  • 动态规划从较小问题的解，有交叠性质，逐步决策出较大问题的解，它是从f(1)往f(10)方向往上推求解，所以称为自底向上的解法。
  • 动态规划有几个典型得特征，最优子结构，状态转移方程，边界，重叠子问题。

例如：

  • f(n-1)和f(n-2) 称为 f(n) 的最优子结构
  • f(n)= f（n-1）+f（n-2）就称为状态转移方程
  • f(1) = 1, f(2) = 2 就是边界啦
  • 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。
public class Solution {
    public int numWays(int n) {
        if (n<= 1) {
            return 1;
        }
        if (n == 2) {
            return 2;
        }
        int a = 1;
        int b = 2;
        int temp = 0;
        for (int i = 3; i <= n; i++) {
            temp = (a + b)% 1000000007;
            a = b;
            b = temp;
        }
        return temp;
    }
    }

动态规划解题思路

  1. 在问题中，可以把所有可能穷举出来，发现有重叠子问题得存在，就可以考虑动态规划。

  2. 一些求最值得场景，比如最长递增子序列，最小编辑距离，背包问题，凑零钱问题等，都是经典得动态规划的经典应用场景

  3. 核心就是拆分子问题，记住过往，减少重量计算，总结思路就是：

    • 穷举分析
    • 确认边界
    • 找出规律，确定最优子结构
    • 写出状态转移方程

    1. 穷举分析

    2. 确定边界
      通过穷举分析，我们发现，当台阶数是1的时候或者2的时候，可以明确知道青蛙跳法。f（1） =1，f(2) = 2，当台阶n>=3时，已经呈现出规律f(3) = f(2) + f(1) =3，因此f（1） =1，f(2) = 2就是青蛙跳阶的边界。

    3. 确定最优子结构
      n>=3时，已经呈现出规律 f(n) = f(n-1) + f(n-2) ，因此，f(n-1)和f(n-2) 称为 f(n) 的最优子结构。什么是最优子结构？有这么一个解释：一道动态规划问题，其实就是递推问题。假设当前决策结果是f(n),则最优子结构就是要让f(n-k)最优，最优子结构性质就是能让转移到n的状态最优的，并且与后面的决策没有关系，即让后面的决策安心的使用前面的局部最优解的一种性质.

    4. 写出状态转移方程
      通过前面3步，穷举分析，确定边界，最优子结构，得出状态转移方程：

    5. 代码实现

      dp[0][0][...] = 边界值
      for(状态1 ：所有状态1的值){
       for(状态2 ：所有状态2的值){
           for(...){
             //状态转移方程
             dp[状态1][状态2][...] = 求最值
           }
       }
      }

案例分析

给你一个整数数组nums，找到其中最长严格递增子序列的长度。
输入：nums=[10,9,2,5,3,7,101,18];
输出：4
解释：最长递增子序列是[2,3,7,101],因此长度为

穷举分析

这里观察规律，显然是有关系的，我们还是遵循动态规划自底向上的原则，基于示例1的数据，从数组只有一个元素开始分析。

  • 当nums只有一个元素10时，最长递增子序列是[10],长度是1.
  • 当nums需要加入一个元素9时，最长递增子序列是[10]或者[9],长度是1。
  • 当nums再加入一个元素2时，最长递增子序列是[10]或者[9]或者[2],长度是1。
  • 当nums再加入一个元素5时，最长递增子序列是[2,5],长度是2。
  • 当nums再加入一个元素3时，最长递增子序列是[2,5]或者[2,3],长度是2。
  • 当nums再加入一个元素7时，,最长递增子序列是[2,5,7]或者[2,3,7],长度是3。
  • 当nums再加入一个元素101时，最长递增子序列是[2,5,7,101]或者[2,3,7,101],长度是4。
  • 当nums再加入一个元素18时，最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4。
  • 当nums再加入一个元素7时,最长递增子序列是[2,5,7,101]或者[2,3,7,101]或者[2,5,7,18]或者[2,3,7,18],长度是4.

分析找规律，拆分子问题。

如果新加入一个元素nums[i], 最长递增子序列要么是以nums[i]结尾的递增子序列，要么就是nums[i-1]的最长递增子序列。nums[i]的最长递增子序列，不就是从以数组num[i]每个元素结尾的最长子序列集合，取元素最多（也就是长度最长）。可以用dp[i]表示以num[i]这个数结尾的最长递增子序列的长度

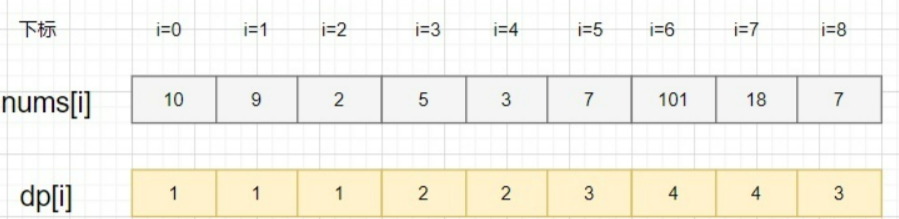
image-20230422155700534

nums[i]结尾的自增子序列，只要找到比nums[i]小的子序列，加上nums[i]

最简单边界情况

当nums数组只有一个元素时候，最长递增子序列的长度dp(1) = 1,当nums数组有两个元素时，dp(2) =2或者1， 因此边界就是dp(1)=1。

确定最优子结构

max(dp(j)) 就是最优子结构。

dp(i) =max(dp(j))+1，存在j属于区间[0，i-1],并且num[i]>num[j]。

状态转移方程

通过前面分析，我们就可以得出

最长递增子序列 =max(dp[i])

代码实现

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length == 0) {
            return 0;
        }
        int[] dp = new int[nums.length];
        //初始化就是边界情况
        dp[0] = 1;
        int maxans = 1;
        //自底向上遍历
        for (int i = 1; i < nums.length; i++) {
            dp[i] = 1;
            //从下标0到i遍历
            for (int j = 0; j < i; j++) {
                //找到前面比nums[i]小的数nums[j],即有dp[i]= dp[j]+1
                if (nums[j] < nums[i]) {
                    //因为会有多个小于nums[i]的数，也就是会存在多种组合了嘛，我们就取最大放到dp[i]
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            //求出dp[i]后，dp最大那个就是nums的最长递增子序列啦
            maxans = Math.max(maxans, dp[i]);
        }
        return maxans;
    }
}