二叉树

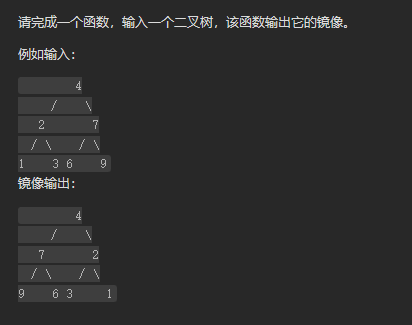
镜像二叉树

1.把左右根交换即可

image-20221219090003177

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if (root == null) return null;
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        mirrorTree(root.left);
        mirrorTree(root.right);
        return root;
    }
}

找出克隆二叉树中的相同节点

image-20221205100529196

public final TreeNode getTargetCopy(final TreeNode original, final TreeNode cloned, final TreeNode target) {
        if (original == null) return null;
        if (original == target) return cloned;
        TreeNode left = getTargetCopy(original.left, cloned.left, target);
        if (left!=null) return left;
        return getTargetCopy(original.right, cloned.right, target);
    }

HomeWork

自定义树结点

public class TreeNode {
     char val;
     TreeNode left;
     TreeNode right;
     TreeNode() {}
     TreeNode(char val) { this.val = val; }
     TreeNode(char val, TreeNode left, TreeNode right) {
         this.val = val;
         this.left = left;
         this.right = right;
     }

1. 先根序列构造二叉树：A B null D null null C null null

//一个全局变量，其实缺点也会很多，对于后面的方法均需要一个计时器，还有一种就是放在方法内的局部变量，跟着方法递归增加
static int count = 0;
//题目给的是字符串，可以用toCharArray()变换字符数组
public TreeNode CteateTree(char[] arr) {
    TreeNode node = null;
    if (count < arr.length) {
        char val = arr[count++];
        //当val值不等于空，这里把^当成空，就把新的带有val的节点赋值给真正意义上的根节点，往后的都是左右子树
        if (val != '^') {
            node = new TreeNode(val);
            node.left = CteateTree(arr);
            node.right = CteateTree(arr);
        }
    }
    //这道题你也简单点理论上可以直接把^也带入结点,不做空值处理,起码在我这里是这样,上面的自定义树节点的基本存储数据类型是用了char.这样好像也可以节省后面遍历的空值处理问题
    return node;
}

2.对于1中生成的二叉树进行前序、中序、后序遍历。

//前序输出
public static void preOrderTravera(TreeNode node){
    if(node!=null) {
        System.out.print(node.val + " ");
        preOrderTravera(node.left);
        preOrderTravera(node.right);
    }
    else {
        System.out.print('^');
        System.out.print(' ');
    }
}
//中序输出
public static void inOrderTravera(TreeNode node){
    if(node != null) {

        inOrderTravera(node.left);
        System.out.print(node.val + " ");
        inOrderTravera(node.right);
    }
    else {
        System.out.print('^');
        System.out.print(' ');
    }
}
//后序输出
public static void postOrderTravera(TreeNode node){
    if(node != null) {
        postOrderTravera(node.left);
        postOrderTravera(node.right);
        System.out.print(node.val + " ");
    }
    else {
        System.out.print('^');
        System.out.print(' ');
    }
}

3. 计算1中生成的二叉树结点总数。

//老样子,静态全局变量,你也可以局部变量,像下面一样,充当一个计数器的作用,只需要在实例方法中输入从0开始,效果是一样的,局部变量的好处就是当你使用完方法后会释放内存,也就是会比一直存在占用内存static全局变量更节省空间.
static int num=0;
//思路很简单,遇到非空值计数器就+1.考虑到前面提到的^直接带入结点,这里还可能要加上值不为^
public int TreeNodeNum(TreeNode node,/*，int num */) {
    if (node != null) {
        num += 1;
        TreeNodeNum(node.left);
        TreeNodeNum(node.right);
    }
    return num;
}

4. 计算1中生成二叉树的高度

//题目的主要问题是怎么在众多的左右子树中找出最大的根深度也就是普遍说的树高
//思路:递归判断,当这个结点为空的时候,则返回0,每次的递归都需要一次深度比较,找出最大的深度
public int maxDepth(TreeNode root) {
    if(root==null){
        return 0;
    }
    else{
        int leftNode =maxDepth(root.left);
        int rightNode=maxDepth(root.right);
        //这里的+1是因为是根节点并没有参与计算,因此需要+上根结点
        return Math.max(leftNode,rightNode)+1;
    }
}

5.计算1中生成二叉树中度为1的节点数、度为2的结点数和叶子数。

//总的思路就是判断左右指针的三种情况即可1.均为空 2.左空右不空(左不空右空)3.均不为空
//叶子结点数
    public int LeafNodeCount(TreeNode root) {
        if (root == null) {
            return 0;
        }
        if (root.left == null && root.right == null) {
            return 1+LeafNodeCount(root.left)+LeafNodeCount(root.right);
        }
        return LeafNodeCount(root.left) + LeafNodeCount(root.right);
    }

    public int OneNodeCount(TreeNode root) {
        if (root == null) {
            return 0;
        }
        if (root.left == null && root.right != null || root.left != null && root.right == null) {
            return 1+OneNodeCount(root.left)+OneNodeCount(root.right);
        }
        return OneNodeCount(root.left) + OneNodeCount(root.right);
    }

    public int DoubleNodeCount(TreeNode root) {
        if (root == null) {
            return 0;
        }
        if (root.right != null && root.left != null) {
            return 1+DoubleNodeCount(root.left) + DoubleNodeCount(root.right);
        }
        return DoubleNodeCount(root.left) + DoubleNodeCount(root.right);
    }

6.按照下面两个序列生成二叉树：先序：ABHFDECKG ；中序：HBDFAEKCG

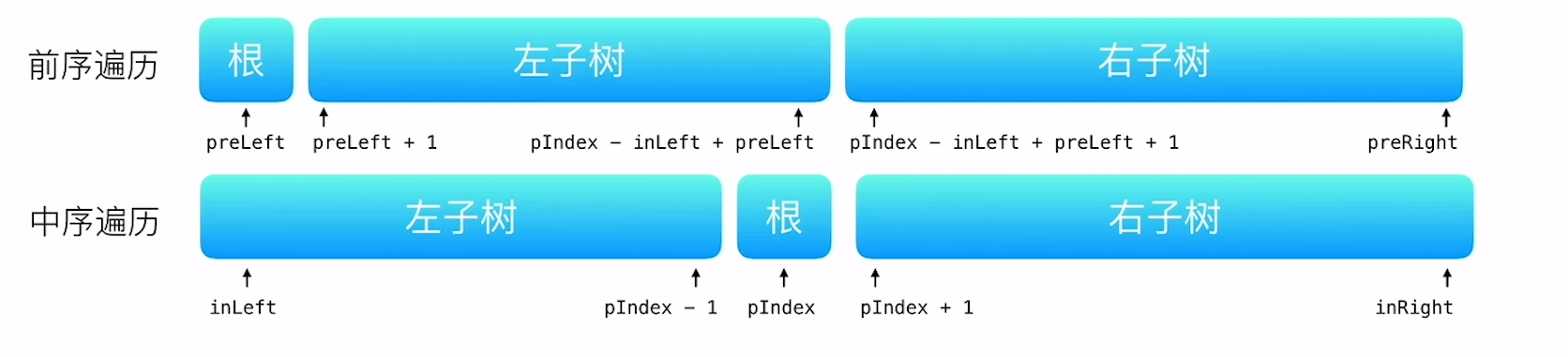
前序+中序构造二叉树
先序:根 [左子树] [右子树]
中序:[左子树] 根 [右子树]

思路:只要遍历中序找到根节点,利用双指针确认左右子树遍历结果的长度,再利用先序方式构造即可

image-20221122113530560

循环寻界+递归构造树

public TreeNode buildTrees(char [] pre,char [] in) {
//构造函数
    TreeNode root=buildTree(pre,0,pre.length-1,in,0,in.length-1);
     return root;
}
//主体
private TreeNode buildTree(char [] pre,int PreLeft,int PreRight,char [] in,int inLeft,int inRight) {
//如果越界则表示结点为空
      if(PreLeft>PreRight||inLeft>inRight)
        return null;
//开始构造,声明新结点
   TreeNode root=new TreeNode(pre[PreLeft]);
//循环寻找中序的根节点,还能够确认左右子树边界
         for(int i=inLeft;i<=inRight;i++){
            if(in[i]==pre[PreLeft]){
//先序构造树,指针就定义为左右子树的区间,构造左子树             
    root.left=buildTree(pre,PreLeft+1,PreLeft+i-inLeft,in,inLeft,i-1);
//变化右子树边界,构造右子树
     root.right=buildTree(pre,i-inLeft+PreLeft+1,PreRight,in,i+1,inRight);
                break;
                }
         }
            return root;
        }

哈希表优化循环子过程

//过程几乎与上面的方法一样，只不过不需要每次递归后又进行循环来找到边界。
//提前把中序的所有遍历用哈希表储存起来即可。后面的取根直接依靠对应值来寻找序号，用来定界
public TreeNode buildTreeTwo(char [] pre,char [] in){
        int PreLen = pre.length;
        int InLen = pre.length;
        Map<Character,Integer> map = new HashMap<>(PreLen);
        for (int i =0;i<InLen;i++){
            map.put(in[i],i);
        }
        return buildTreeTwo(pre,0,PreLen-1,map,0,InLen-1);
        }

private TreeNode buildTreeTwo(char[]pre,int PreLeft,int PreRight,Map<Character,Integer> map,int InLeft,int InRight){
        if(PreLeft>PreRight||InLeft>InRight){
            return null;
        }
        char val = pre[PreLeft];
        TreeNode root = new TreeNode(val);
        int index = map.get(val);
        root.left=buildTreeTwo(pre,PreLeft+1,index-InLeft+PreLeft,map,InLeft,index-1);
        root.right=buildTreeTwo(pre,index-InLeft+PreLeft+1,PreRight,map,index+1,InRight);
        return root;
    }

栈方法迭代

public TreeNode buildTree(char[] preorder, char[] inorder) {
    if (preorder == null || preorder.length == 0) {
        return null;
    }
    TreeNode root = new TreeNode(preorder[0]);
    Deque<TreeNode> stack = new LinkedList<TreeNode>();
    stack.push(root);
    int inorderIndex = 0;
    for (int i = 1; i < preorder.length; i++) {
        int preorderVal = preorder[i];
        TreeNode node = stack.peek();
        if (node.val != inorder[inorderIndex]) {
            node.left = new TreeNode(preorderVal);
            stack.push(node.left);
        } else {
            while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
                node = stack.pop();
                inorderIndex++;
            }
            node.right = new TreeNode(preorderVal);
            stack.push(node.right);
        }
    }
    return root;
}

二叉树遍历

建立树节点

public class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode(){}
TreeNOde(int val){
this val = val;
}
TreeNode(int val,TreeNode left,TreeNode right){
this.val = val;
this.left=left;
this.right=right;
}
}

前序遍历

public static void preOrderTraveral(TreeNode node){
if(node==null){
return;
}
System.out.print(node.data+"");
preOrderTraveral(node.left);
preOrderTraveral(node.right);
}

中序遍历

public static void inOrderTraveral(TreeNode node){
if(node == null){
return;
}
inOrderTraveral(node.left);
System.out.print(node.data+"");
inOrderTraveral(node.right);
}

后序遍历

public static void postOrderTraveral(TreeNode node){
if(node == null){
return;
}
postTraveral(node.left);
postTraveral(node.right);
System.out.print(node.data+"");
}

层次遍历

public void leverOrder(TreeNode root) {
        //声明一个队列对象
        Queue<TreeNode> storage = new LinkedList<TreeNode>();
        // 根节点为空，返回空值
        if (root == null) {
            return;
        }
        //把结点拉入队列
        storage.offer(root);
        while(!storage.isEmpty()){
        //把队列首部拉出输出值并且访问左右子树结点
            TreeNode cur = storage.poll();
            System.out.print(cur.val+" ");
            //若左指针不为空，就把左子树拉入队列
            if (cur.left!=null){
                storage.offer(cur.left);
            }
            //若右指针不为空，就把右子树拉入队列
            if (cur.right!=null) {
                storage.offer(cur.right);
            }
        }
    }

Morris遍历

https://zitiu.top/2022/10/24/Morris%20%E9%81%8D%E5%8E%86/

leetcode

总思路

  1. 只要提到树的话就几乎都会涉及到递归和回溯.

  2. 比较常用的算法思想就是深度和广度优先搜索

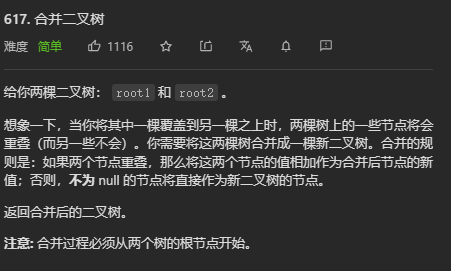
    617.合并二叉树

  3. 这道题我的思路很简单,就是递归遍历,进行创新节点的操作

  4. 可以分三种情况

    • 两个节点均为null值
    • 一个节点为null,一个不为null值
    • 两个节点都不是null值

image-20221112162114118

实现1:深度优先搜索

public TreeNode merageTrees(TreeNode r1,TreeNode r2){
   if(r1==null) return r2;
   if(r2==null) return r1;
   TreeNode metaTree = new TreeNode(r1.val+r2.val);
   metaTree.left = merageTrees(r1.left,r2.left);
   metaTree.right= merageTrees(r1.right,r2.right);
   return metaTree;
}

实现2:广度优先搜索

  1. 主要实现:构建三个队列分别储存3颗树的每个节点
  • 每次从队列种取出一个节点,判断两个原始树的结点是否为空
     public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
          if (t1 == null) {
              return t2;
          }
          if (t2 == null) {
              return t1;
          }
          TreeNode merged = new TreeNode(t1.val + t2.val);
          Queue<TreeNode> queue = new LinkedList<TreeNode>();
          Queue<TreeNode> queue1 = new LinkedList<TreeNode>();
          Queue<TreeNode> queue2 = new LinkedList<TreeNode>();
          queue.offer(merged);
          queue1.offer(t1);
          queue2.offer(t2);
          while (!queue1.isEmpty() && !queue2.isEmpty()) {
              TreeNode node = queue.poll(), node1 = queue1.poll(), node2 = queue2.poll();
              TreeNode left1 = node1.left, left2 = node2.left, right1 = node1.right, right2 = node2.right;
              if (left1 != null || left2 != null) {
                  if (left1 != null && left2 != null) {
                      TreeNode left = new TreeNode(left1.val + left2.val);
                      node.left = left;
                      queue.offer(left);
                      queue1.offer(left1);
                      queue2.offer(left2);
                  } else if (left1 != null) {
                      node.left = left1;
                  } else if (left2 != null) {
                      node.left = left2;
                  }
              }
              if (right1 != null || right2 != null) {
                  if (right1 != null && right2 != null) {
                      TreeNode right = new TreeNode(right1.val + right2.val);
                      node.right = right;
                      queue.offer(right);
                      queue1.offer(right1);
                      queue2.offer(right2);
                  } else if (right1 != null) {
                      node.right = right1;
                  } else {
                      node.right = right2;
                  }
              }
         }
         return merged;
    }

100.相同的树

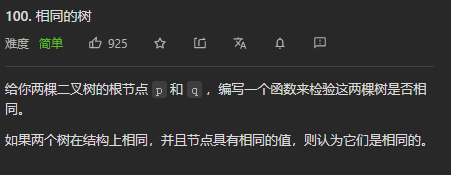
image-20221112184055309

  1. 树的递归判断
public boolean isSameTree(TreeNode p,TreeNode q){
if(p==null&&q==null) return true;
if(p==null||q==null) return false;
if(p.val!=q.val) return false;
return isSameTree(p,left,q.left)&&isSameTree(p.right,q.right);
}

对称二叉树

image-20221112184440687

  1. 基本和相同树的判断思想是一样的，只要把左右两个孩子分别当作新的结点进行比较
public boolean isSymmetric(TreeNode root) {
     return  isSameTree(root,root);
   }
   public boolean isSameTree(TreeNode leftnode,TreeNode rightnode){
       if(leftnode==null&&rightnode==null){
           return true;
       }
       if(leftnode==null||rightnode==null){
           return false;
       }
       return leftnode.val==rightnode.val&&isSameTree(leftnode.left,rightnode.right)&&isSameTree(leftnode.right,rightnode.left);
   }

226.翻转二叉树

image-20221112184924806

  1. 思路也是十分的简单，像数组的位置变换一样，定义一个辅助变量，而这边定义一个新的树对象来储存。
// 思想十分像数组的辅助变量位置变换的方法
       public TreeNode invertTree(TreeNode root) {
           if (root == null) return null;
           // 声明一个新的对象，先是储存右孩子的数据
           TreeNode rightTree = root.right;
           root.right = invertTree(root.left);
           root.left = invertTree(rightTree);
           return root;
       }

111.二叉树的最小深度

  1. 做法几乎于最大深度差不多，只是把max改成min罢了
  2. 但是要注意的是空节点是不需要比较的。

image-20221113135809932

pubilc int minDepth(TreeNode root){
if(root==null){
return 0;
}
if(root.right==null&&root.left!=null){
return 1+minDepth(root.left);
}
if(root.left==null&&root.right!=null){
return 1+minDepth(root.right);
}
return Math.min(minDepth(root.left),minDepth(root.right))+1;
}

637.二叉树的层平均值

  1. 我第一反应是一定要用到层次遍历，那么每层的结点个数我是应该怎么确定呢？
  2. 然而实际上确实需要用到层次遍历的思想，而且还需要一个计数器

image-20221123191353894

public List<Double> averageOfLevels(TreeNode root) {
       List<Double> storage = new ArrayList<Double>();
       Queue<TreeNode> stoge = new LinkedList<TreeNode>();
       stoge.offer(root);
       while(!stoge.isEmpty()){
           double sum = 0.0;
           int size = stoge.size();
           for(int i = 0;i<size;i++){
               root = stoge.poll();
               sum += root.val;
           if(root.left!=null){
               stoge.offer(root.left);
           }
           if(root.right!=null){
               stoge.offer(root.right);
           }
       }
       storage.add(sum/size);
       }
       return storage;
   }
  1. 步骤解析
    1. 在while之前把根结点代入队列。
    2. 开始while循环，重置sum值，目的是为了把每层的的结点总值区分开添入List中
    3. 获取队列的长度，队列的长度在这里其实就是这层结点的总数
    4. 比如代入root后，然后元素出队，因为此时的队列中只有root一个元素，所以出队root后，队列为空，停止循环，然后计算sum值，sum值得计算是用for循环本层得结点数得次数后得到得，然后把sum/size添加入List中
    5. 判断，那么两个if语句为了让下一个左右结点得入队，空则不入，不空则入。

404.左子叶之和

image-20221125104925282

  1. 首先需要的是找到叶子节点，如果是就回溯到上一个结点输出左子叶，如果不是的话就往下递归。
    1. 递归
      public int sumOfLeftLeaves(TreeNode root) {
             int sum = 0;
             if(root==null){
                 return 0;
             }
             if(root.left!=null&&root.left.right==null&&root.left.left==null){
                 sum += root.left.val;
             }
             return sumOfLeftLeaves(root.left)+sumOfLeftLeaves(root.right)+sum;
         }
    2. 队列（广度优先搜索）
      public int sumOfLeftLeaves(TreeNode root) {
          Queue<TreeNode> storage = new LinkedList<TreeNode>();
          int sum = 0;
          storage.offer(root);
          if (root == null) {
              return 0;
          }
          while(!storage.isEmpty()){
              TreeNode node = storage.poll();
              if(node.left!=null){
                  if(node.left.right==null&&node.left.left==null){
                      sum+=node.left.val;
                  }
                  else{
                      storage.offer(node.left);
                  }
              }
              if(node.right!=null){
                  if(!(node.right.left==null&&node.right.right==null)){
                      storage.offer(node.right);
                  }
              }
          }
          return sum;
      }