图存结构
图的存储结构
基本知识(此次都是为图存储结构的基本知识,若已了解可跳至算法部分)
什么是图存储结构
- 根据有向和无向线来连接每个顶点间的关系
- 有向图:如果元素之间存在单向的联系,那么这样的图结构称为有向图.
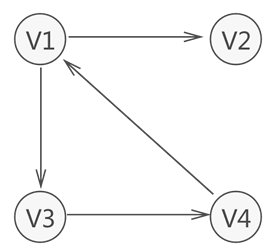
- 无向图:各个元素之间的联系都是双向的,这样的图存结构称为无向图。
- 有向图:如果元素之间存在单向的联系,那么这样的图结构称为有向图.
图的基本概念
1.弧头和弧尾
- 有向图中,无箭头的一端的顶点通常被称为“初始点”或“弧尾”,箭头的一段被称为“终端点”或“弧头”。
2.入度和出度
- 对于有向图中的一个顶点 V 来说,箭头指向 V 的弧的数量为 V 的入度(InDegree,记为 ID(V));箭头远离 V 的弧的数量为 V 的出度(OutDegree,记为OD(V))。
3.(V1,V2)和<V1,V2>的区别
- 无向图中描述两顶点V1和V2之间的关系可以用(V1,V2)来表示;有向图中描述从V1到V2的“单向”关系可以用<V1,V2>来表示
- 由于图存储结构中顶点之间的关系是可以用线来表示的,因此(V1,V2)还可以用来表示无向图中连接V1和V2的线,又称为边;同样<V1,V2>也可用来表示有向图中从V1到V2带方向的线,又称为弧。
4.集合VR
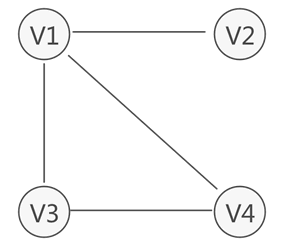
- 图中习惯用VR表示图中所有顶点之间的关系的集合,例如,上图无向图的集合VR={(V1,V2),(V1,V4),(V1,V3),(V3,V4)}。有向图的集合 VR={<v1,v2>,<v1,v3>,<v3,v4>,<v4,v1>}。
5.路径和回路
- 无论是无向图还是有向图,从一个顶点到另一个顶点途径的所有顶点组成的序列(包括起点和终点),称为一条路径。若路径中的某个顶点能够最后回到自己身上,那么这个路径称为环或者回路
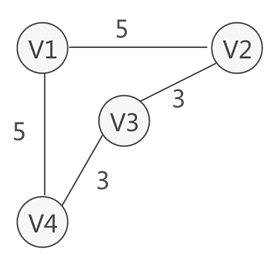
6.权和网
- 在一些图中,可能为每条边赋值一个实数表示一定的含义,这种与边(或弧)相互匹配的实数被称为“权”,而带权的图通常称为网。例如,图4就是一个网结构:
7.子图
- 指的是由图中一部分顶点和边构成的图称为原图的子图
分类
完全图
- 每个顶点都有与除开自身外的其他顶点有直接关系
- 若有n个顶点的完全图,则图中边的数量为n(n-1)/2;而对于具有n个顶点的有向完全图,图中的弧的数量为n(n-1)。
连通图
- 如果图中从一个顶点到达另外一个顶点,至少有一条路径,那么这两个顶点是连通着的。例如图中,虽然V1和V3没有直接关联,但从V1到V3存在两条路径,分别是V1-V2-V3和V1-V4-V3,因此称V1和V2之间是连通的
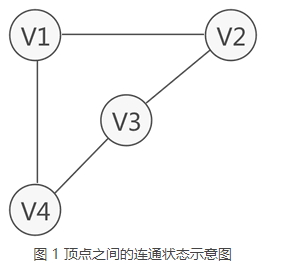
上面用的是无向图的例子,其实有向图也是基本差不多的啦,自己揣摩哦!!!!强连通图
- 在有向图中两个顶点彼此都有至少有一条通路,那么这有向图为强连通图。
- 除此之外,若有向图不是强连通图,但其中包含的是最大连通子图具有强连通的性质,则称该子图为强连通分量
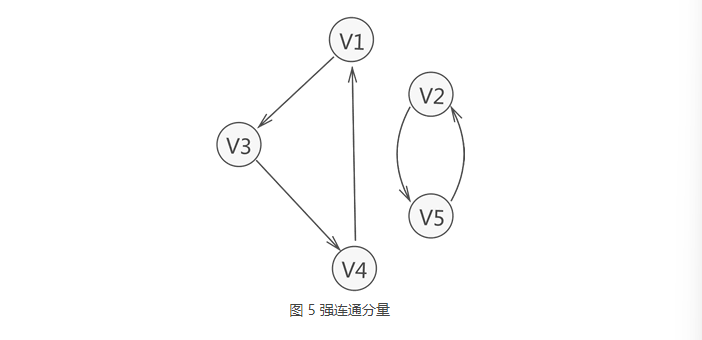
生成树
- 其实对连通图的遍历的过程中就已经是生成树的过程了
1.如图: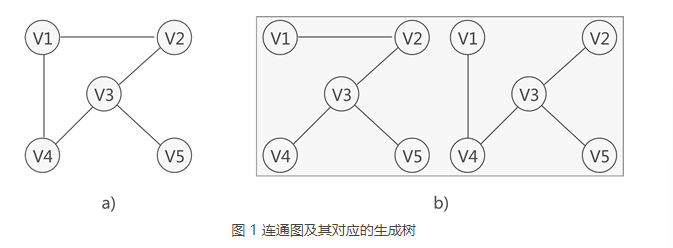
2.需要注意的是连通图中,由于任意两顶点之间可能含有多条通路,遍历连通图的方式有多种,往往一张连通图可能有多种不同的生成树与之对应。
3.连通图中的生成树必须满足以下 2 个条件:- 包含连通图中所有的顶点;
- 任意两顶点之间有且仅有一条通路;
编程实现
图的顺序存储结构
- 虽然图结构的数据元素存在多对多关系,但是同样可以采用顺序储存,能够使用数组有效的储存图
- 需要注意的是:数组储存图时,需要一个数组存放图中顶点本身的数据(最好是一维数组),另外一个数组存储的是各顶点之间的关系(这时候就要是二维数组了)
邻接矩阵无向图
public class MatrixNDG {
int size;//图顶点个数
char[] vertexs;//图顶点名称
int[][] matrix;//图关系矩阵
public MatrixNDG(char[] vertexs,char[][] edges){
size=vertexs.length;
matrix=new int[size][size];//设定图关系矩阵大小
this.vertexs=vertexs;
for(char[] c:edges){//设置矩阵值
int p1 = getPosition(c[0]);//根据顶点名称确定对应矩阵下标
int p2 = getPosition(c[1]);
matrix[p1][p2] = 1;//无向图,在两个对称位置存储
matrix[p2][p1] = 1;
}
}
//图的遍历输出
public void print(){
for(int[] i:matrix){
for(int j:i){
System.out.print(j+" ");
}
System.out.println();
}
}
//根据顶点名称获取对应的矩阵下标
private int getPosition(char ch) {
for(int i=0; i<vertexs.length; i++)
if(vertexs[i]==ch)
return i;
return -1;
}
public static void main(String[] args) {
char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K'};
char[][] edges = new char[][]{
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'D', 'G'},
{'I','J'},
{'J','G'},};
MatrixNDG pG;
// 自定义"图"(输入矩阵队列)
// 采用已有的"图"
long start=System.nanoTime();
for(int i=0;i<10000;i++){
pG = new MatrixNDG(vexs, edges);
//pG.print(); // 打印图
}
long end=System.nanoTime();
System.out.println(end-start);
}
}邻接矩阵有向图
public class MatrixDG {
int size;
char[] vertexs;
int[][] matrix;
public MatrixDG(char[] vertexs,char[][] edges){
size=vertexs.length;
matrix=new int[size][size];
this.vertexs=vertexs;
//和邻接矩阵无向图差别仅仅在这里
for(char[] c:edges){
int p1 = getPosition(c[0]);
int p2 = getPosition(c[1]);
matrix[p1][p2] = 1;
}
}
public void print(){
for(int[] i:matrix){
for(int j:i){
System.out.print(j+" ");
}
System.out.println();
}
}
private int getPosition(char ch) {
for(int i=0; i<vertexs.length; i++)
if(vertexs[i]==ch)
return i;
return -1;
}
public static void main(String[] args) {
char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K'};
char[][] edges = new char[][]{
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'D', 'G'},
{'I','J'},
{'J','G'},};
MatrixDG pG;
// 自定义"图"(输入矩阵队列)
//pG = new MatrixUDG();
// 采用已有的"图"
pG = new MatrixDG(vexs, edges);
pG.print();
}
}邻接表无向表
public class ListNDG {
Vertex[] vertexLists;//邻接表数组
int size;
class Vertex{//邻接表节点类,单链表数据结构
char ch;
Vertex next;
Vertex(char ch){//初始化方法
this.ch=ch;
}
void add(char ch){//加到链表尾
Vertex node=this;
while(node.next!=null){
node=node.next;
}
node.next=new Vertex(ch);
}
}
public ListNDG(char[] vertexs,char[][] edges){
size=vertexs.length;
this.vertexLists=new Vertex[size];//确定邻接表大小
//设置邻接表头节点
for(int i=0;i<size;i++){
this.vertexLists[i]=new Vertex(vertexs[i]);
}
//存储边信息
for(char[] c:edges){
int p1=getPosition(c[0]);
vertexLists[p1].add(c[1]);
int p2=getPosition(c[1]);
vertexLists[p2].add(c[0]);
}
}
//跟据顶点名称获取链表下标
private int getPosition(char ch) {
for(int i=0; i<size; i++)
if(vertexLists[i].ch==ch)
return i;
return -1;
}
//遍历输出邻接表
public void print(){
for(int i=0;i<size;i++){
Vertex temp=vertexLists[i];
while(temp!=null){
System.out.print(temp.ch+" ");
temp=temp.next;
}
System.out.println();
}
}
public static void main(String[] args){
char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K'};
char[][] edges = new char[][]{
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'D', 'G'},
{'I','J'},
{'J','G'},};
ListNDG pG;
long start=System.nanoTime();
for(int i=0;i<10000;i++){
pG = new ListNDG(vexs, edges);
//pG.print(); // 打印图
}
long end=System.nanoTime();
System.out.println(end-start);
}
}邻接有向表
public class ListDG {
Vertex[] vertexLists;
int size;
class Vertex{
char ch;
Vertex next;
Vertex(char ch){
this.ch=ch;
}
void add(char ch){
Vertex node=this;
while(node.next!=null){
node=node.next;
}
node.next=new Vertex(ch);
}
}
public ListDG(char[] vertexs,char[][] edges){
size=vertexs.length;
this.vertexLists=new Vertex[size];
for(int i=0;i<size;i++){
this.vertexLists[i]=new Vertex(vertexs[i]);
}
for(char[] c:edges){
int p=getPosition(c[0]);
vertexLists[p].add(c[1]);
}
}
private int getPosition(char ch) {
for(int i=0; i<size; i++)
if(vertexLists[i].ch==ch)
return i;
return -1;
}
public void print(){
for(int i=0;i<size;i++){
Vertex temp=vertexLists[i];
while(temp!=null){
System.out.print(temp.ch+" ");
temp=temp.next;
}
System.out.println();
}
}
public static void main(String[] args){
char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G','H','I','J','K'};
char[][] edges = new char[][]{
{'A', 'C'},
{'A', 'D'},
{'A', 'F'},
{'B', 'C'},
{'C', 'D'},
{'E', 'G'},
{'D', 'G'},
{'I','J'},
{'J','G'},};
ListDG pG;
long start=System.nanoTime();
for(int i=0;i<10000;i++){
pG = new ListDG(vexs, edges);
//pG.print(); // 打印图
}
long end=System.nanoTime();
System.out.println(end-start);
}
}
DFS
所谓图的遍历,简单理解就是逐个访问图中的顶点,确保每个顶点都只访问一次
深度优先搜索算法遍历图1无向图的过程:
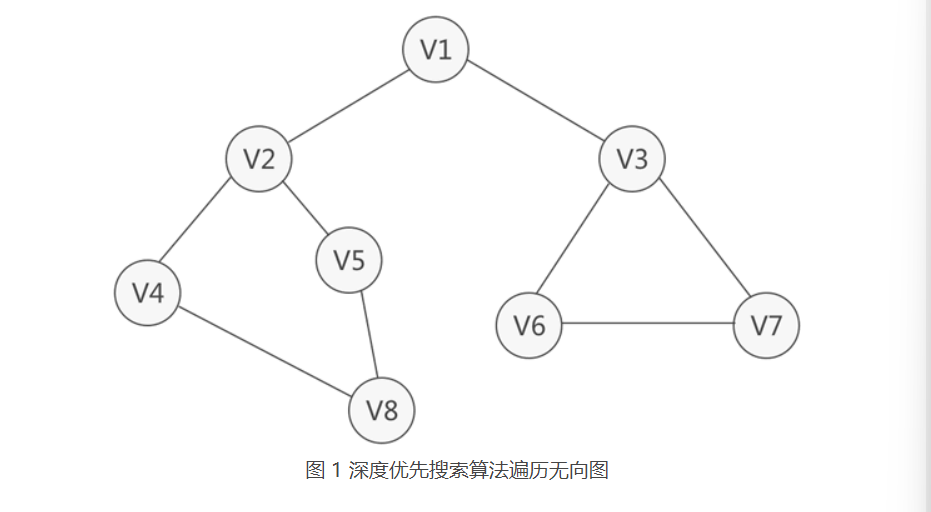
1.初始状态下,无向图中的所有顶点都是没有被访问过的,一次可以任选一个顶点出发,遍历整个无向图,假设从V1顶点开始,先访问V1顶点。
2.紧邻V1的顶点有两个,分别是V2和V3,它们都没有被访问过,从它们中任选一个,这里选择V2
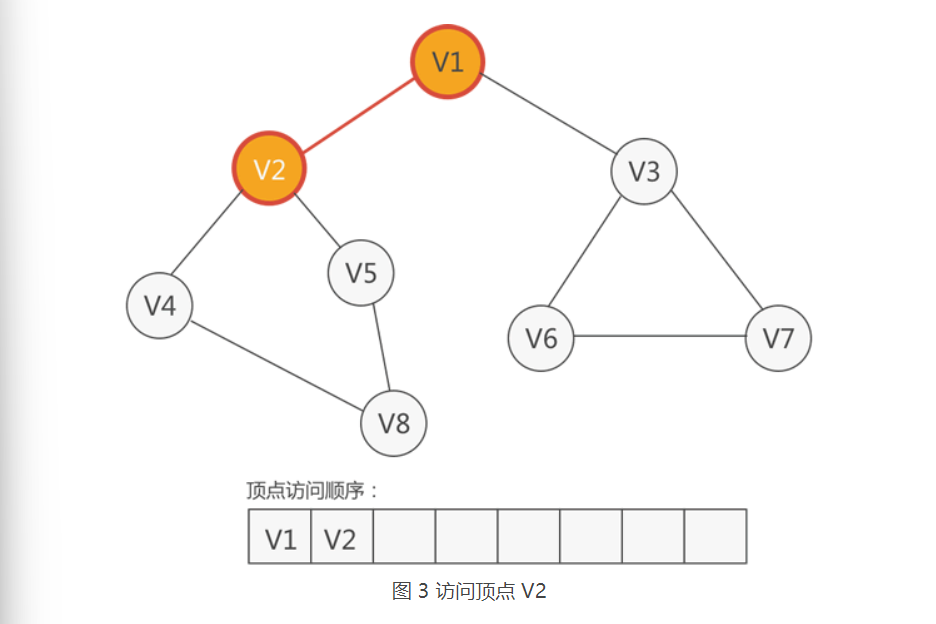
3.紧邻V2的顶点三个,分别是V1,V4,V5,尚未被访问的有V4,V5,从它们中任选一个,比如访问V4,如下图所示:
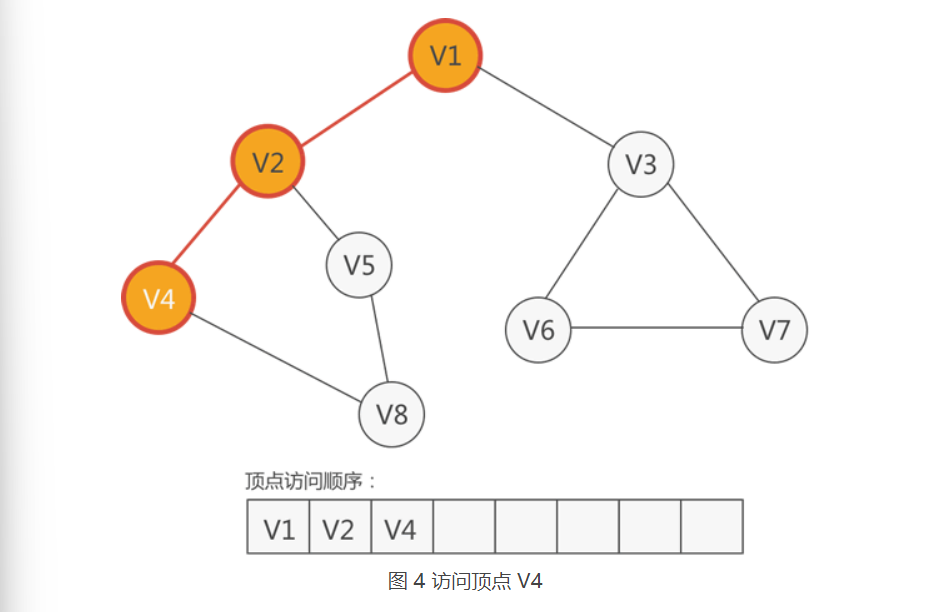
4.紧邻 V4 的顶点有两个,分别是 V2 和 V8,只有 V8 尚未被访问,因此访问 V8,如下图所示:
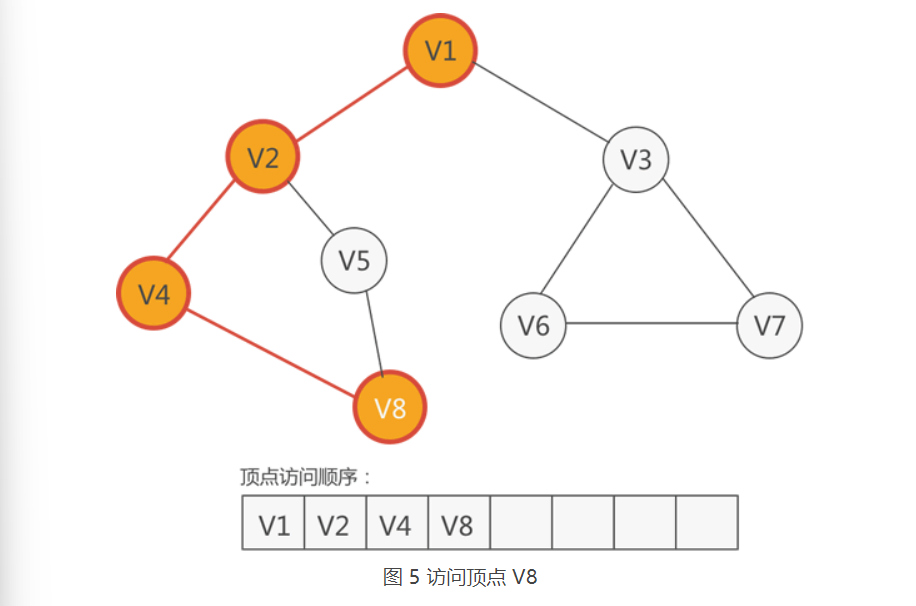
5.紧邻 V8 的顶点有两个,分别是 V4 和 V5,只有 V5 尚未被访问,因此访问 V5,如下图所示:
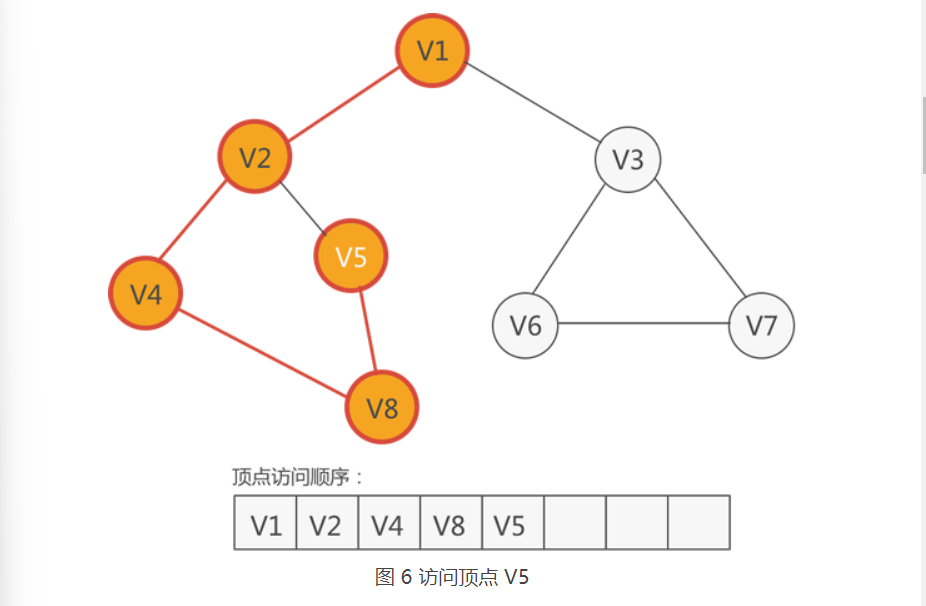
6.和 V5 相邻的顶点有两个,分别是 V2 和 V8,它们都已经访问过了。也就是说,此时从 V5 出发,找不到任何未被访问的顶点了。
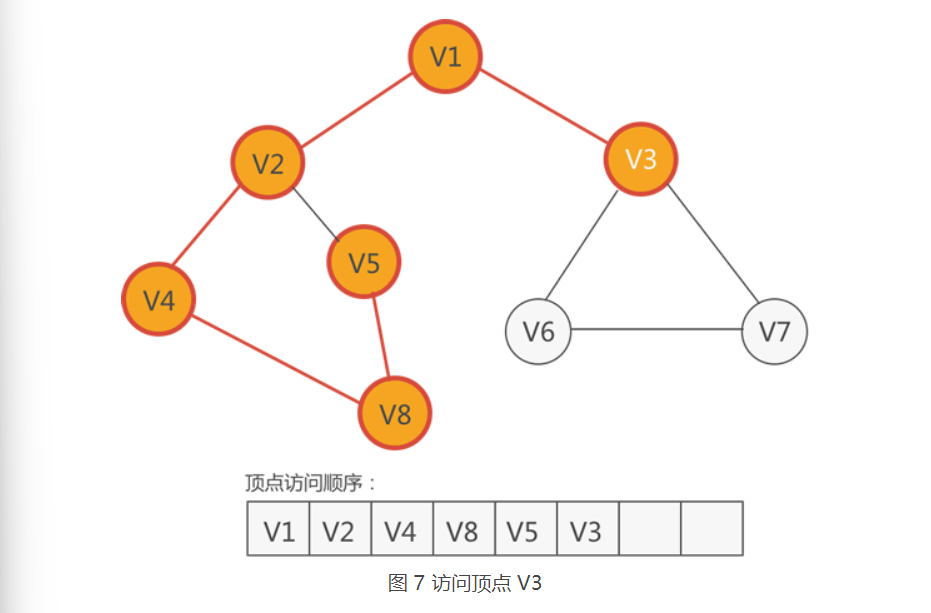
7.这种情况下,深度优先搜索算法会回退到之前的顶点,查看先前有没有漏掉的、尚未访问的顶点:
- 从 V5 回退到 V8,找不到尚未访问的顶点;
- 从 V8 回退到 V4,还是找不到尚未访问的顶点;
- 从 V4 回退到 V2,也还是找不到尚未访问的顶点;
- 从 V2 回退到 V1,发现 V3 还没有被访问。
于是,下一个要访问的顶点就是 V3,如下图所示:
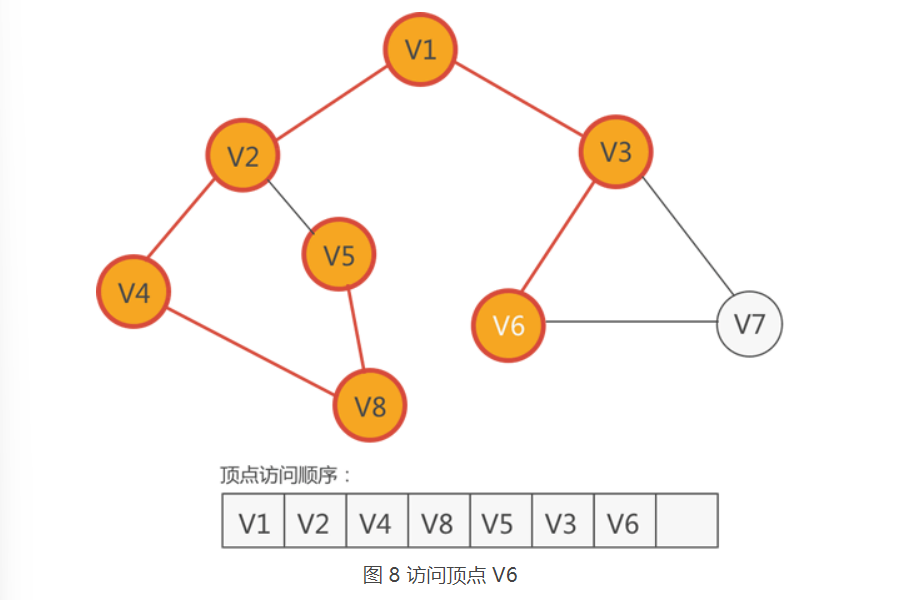
8.紧邻 V3 的顶点有三个,分别是 V1、V6 和 V7,尚未访问的有 V6 和 V7,因此从它们中任选一个,比如访问 V6,如下图所示:
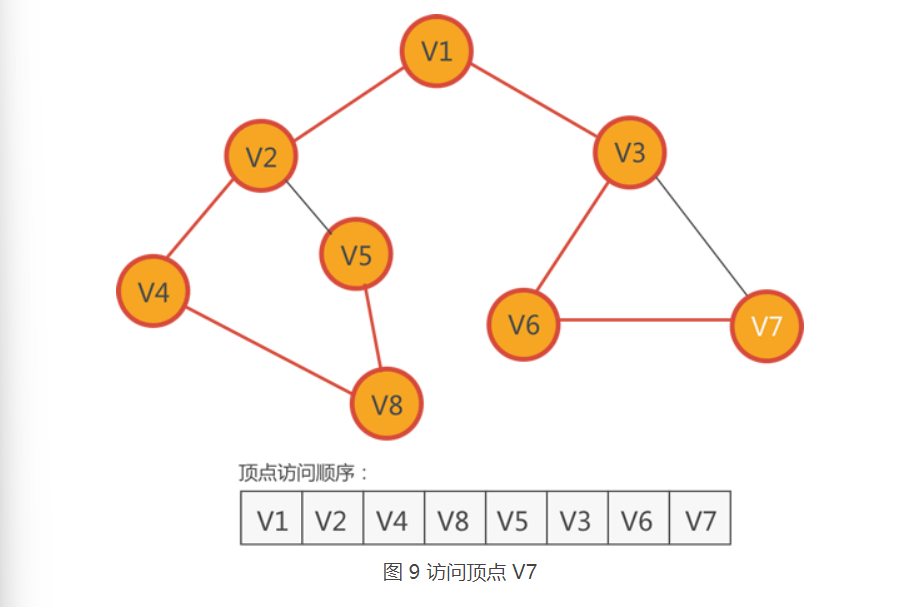
9.紧邻 V6 的顶点有两个,分别是 V3 和 V7,只有 V7 还没有访问,因此访问 V7,如下图所示:
10.紧邻 V7 顶点有 V6 和 V3,但它们都已经访问过了,此时面临的情况和第 6 步完全一样,深度优先搜索算法的解决方法也是一样的:
- 从 V7 回退到 V6,依然找不到尚未访问的顶点;
- 从 V6 回退到 V3,依然找不到尚未访问的顶点;
- 从 V3 回退到 V1,依然找不到尚未访问的顶点;
- V1 是遍历图的起始顶点,回退到 V1 还找不到尚未访问的顶点,意味着以 V1 顶点为突破口,能访问的顶点全部已经访问完了。这种情况下,深度优先搜索算法会从图的所有顶点中重新选择一个尚未访问的顶点,从该顶点出发查找尚未访问的其它顶点。
从图 9 可以看到,图中已经没有尚未访问的顶点了,此时深度优先搜索算法才执行结束。
本部落格所有文章除特別聲明外,均採用 CC BY-NC-SA 4.0 許可協議。轉載請註明來自 Kalyan的小书房!
評論

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)